| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
7.27 three
This module fully extends the notion of guides and paths in Asymptote
to three dimensions. It introduces the new types guide3, path3, and surface.
Guides in three dimensions are specified with the same syntax as in two
dimensions except that triples (x,y,z) are used in place of pairs
(x,y) for the nodes and direction specifiers. This
generalization of John Hobby's spline algorithm is shape-invariant under
three-dimensional rotation, scaling, and shifting, and reduces in the
planar case to the two-dimensional algorithm used in Asymptote,
MetaPost, and MetaFont [cf. J. C. Bowman, Proceedings in
Applied Mathematics and Mechanics, 7:1, 2010021-2010022 (2007)].
For example, a unit circle in the XY plane may be filled and drawn like this:
import three; size(100); path3 g=(1,0,0)..(0,1,0)..(-1,0,0)..(0,-1,0)..cycle; draw(g); draw(O--Z,red+dashed,Arrow3); draw(((-1,-1,0)--(1,-1,0)--(1,1,0)--(-1,1,0)--cycle)); dot(g,red);
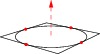
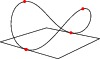
and then distorted into a saddle:
import three; size(100,0); path3 g=(1,0,0)..(0,1,1)..(-1,0,0)..(0,-1,1)..cycle; draw(g); draw(((-1,-1,0)--(1,-1,0)--(1,1,0)--(-1,1,0)--cycle)); dot(g,red);
Module three provides constructors for converting two-dimensional
paths to three-dimensional ones, and vice-versa:
path3 path3(path p, triple plane(pair)=XYplane); path path(path3 p, pair P(triple)=xypart);
A Bezier surface, the natural two-dimensional generalization of Bezier
curves, is defined in three_surface.asy as a structure
containing an array of Bezier patches. Surfaces may drawn with one of
the routines
void draw(picture pic=currentpicture, surface s, int nu=1, int nv=1,
material surfacepen=currentpen, pen meshpen=nullpen,
light light=currentlight, light meshlight=light);
void draw(picture pic=currentpicture, surface s, int nu=1, int nv=1,
material[] surfacepen, pen meshpen,
light light=currentlight, light meshlight=light);
void draw(picture pic=currentpicture, surface s, int nu=1, int nv=1,
material[] surfacepen, pen[] meshpen=nullpens,
light light=currentlight, light meshlight=light);
The parameters nu and nv specify the number of subdivisions
for drawing optional mesh lines for each Bezier patch.
Here material is a structure defined in three_light.asy:
struct material {
pen[] p; // diffusepen,ambientpen,emissivepen,specularpen
real opacity;
real shininess;
real granularity;
...
}
These material properties are used to implement OpenGL-style lighting,
based on the Phong-Blinn specular model. Sample Bezier surfaces are
contained in the example files BezierSurface.asy, teapot.asy,
and parametricsurface.asy.
The examples
elevation.asy and sphericalharmonic.asy
illustrate how to draw a surface with patch-dependent colors.
The examples vertexshading and smoothelevation illustrate
vertex-dependent colors, which is supported for both
the OpenGL renderer and two-dimensional projections.
Since the PRC output format does not support vertex shading of
Bezier surfaces, PRC patches are shaded with the mean of the
four vertex colors.
There is no fill command for arbitrary three-dimensional cyclic paths
(this would be an ill-posed operation).
However, a surface constructed from a convex path3 with the constructor
surface surface(path3 external, triple[] internal=new triple[],
triple[] normals=new triple[], pen[] colors=new pen[]);
and then filled:
draw(surface(path3(polygon(5))),red);
draw(surface(unitcircle3),red);
draw(surface(unitcircle3,new pen[] {red,green,blue,black}));
The last example constructs a patch with vertex-specific colors.
Alternatively, a three-dimensional planar path constructed from a
two-dimensional (possibly nonconvex) cyclic and nonselfintersecting path
p can be filled by first using Orest Shardt's bezulate routine
to decompose p into an array of cyclic paths of length 4
or less. This array can then be used to construct and draw a planar
surface:
draw(surface(bezulate((0,0)--E+2N--2E--E+N..0.2E..cycle)),red);
The routine surface planar(path3 p) uses bezulate to convert
a three-dimensional planar (possibly nonconvex) cyclic and
nonselfintersecting path to a surface.
Arbitrary thick three-dimensional curves and line caps (which the
OpenGL standard does not require implementations to provide) are
constructed with the routine
surface tube(path3 g, real width);
which returns a tube of diameter width centered on g.
This can make files slow to render,
especially with the Adobe Reader renderer. The setting
thick=false can be used to disable this feature and force all
lines to be drawn with linewidth(0) (one pixel wide, regardless
of the resolution). By default mesh and contour lines in three-dimensions
are always drawn thin, unless an explicit linewidth is given in the pen
parameter or the setting thin is set to false. The pens
thin() and thick() defined in plain_pens.asy can also be used
to override these defaults for specific draw commands.
There are four choices for viewing 3D Asymptote output:
- Use the default
AsymptoteadaptiveOpenGL-based renderer (with the command-line option-Vand the default settingsoutformat=""andrender=-1). If you encounter warnings from your graphics card driver, try specifying-glOptions=-indirecton the command line. OnUNIXsystems with graphics support for multisampling, we recommend installing the latest SVN (antialiased) version of thefreeglutlibrary (see multisampling); the sample width can be controlled with the settingmultisample. An initial screen position can be specified with the pair settingposition, where negative values are interpreted as relative to the corresponding maximum screen dimension. The mouse bindings are:- Left: rotate
- shift Left: zoom
- ctrl Left: shift
- Middle: menu
- Wheel: zoom
- Right: zoom
- Right double click: menu
- shift Right: rotate about the X axis
- ctrl Right: rotate about the Y axis
- alt Right: rotate about the Z axis
- h: home
- f: toggle fitscreen
- x: spin about the X axis
- y: spin about the Y axis
- z: spin about the Z axis
- s: stop spinning
- m: rendering mode (solid/mesh/patch)
- e: export
- +: expand
- =: expand
- -: shrink
- _: shrink
- q: exit
- Ctrl-q: exit
- Render the scene to a specified rasterized format
outformatat the resolution ofnpixels perbp, as specified by the settingrender=n. A negative value ofnis interpreted as|2n|for EPS and PDF formats and|n|for other formats. The default value ofrenderis -1. By default, the scene is internally rendered at twice the specified resolution; this can be disabled by settingantialias=1. High resolution rendering is done by tiling the image. If your graphics card allows it, the rendering can be made more efficient by increasing the maximum tile sizemaxtilebeyond the screen dimensions (indicated bymaxtile=(0,0). The tile size is also limited by the settingmaxviewport, which restricts the maximum width and height of the viewport. OnUNIXsystems some graphics drivers support batch mode (-noV) rendering in an iconified window; this can be enabled with the settingiconify=true. OtherUNIXgraphics drivers may require the command line setting-glOptions=-indirect. - Embed the 3D PRC format in a PDF file
and view the resulting PDF file with
version
8.0or later ofAdobe Reader. In addition to the defaultsettings.prc=true, this requiressettings.outformat="pdf", which can be specified by the command line option-f pdf, put in theAsymptoteconfiguration file (see configuration file), or specified in the script beforethree.asy(orgraph3.asy) is imported. Version 2008/10/08 or later of themovie15package is also required (see sectionembed). A stationary preview image with a resolution ofnpixels perbpcan be embedded with the settingrender=n; this allows the file to be viewed with otherPDFviewers. Alternatively, the fileexternalprc.texillustrates how the resulting PRC and rendered image files can be extracted and processed in a separateLaTeXfile. However, seeLaTeXusage for an easier way to embed three-dimensionalAsymptotepictures withinLaTeX. The open-source PRC specification is available from http://livedocs.adobe.com/acrobat_sdk/9/Acrobat9_HTMLHelp/API_References/PRCReference/PRC_Format_Specification/ - Project the scene to a two-dimensional vector (EPS or
PDF) format with
render=0. Only limited hidden surface removal facilities are currently available with this approach (see PostScript3D).
Automatic picture sizing in three dimensions is accomplished with double deferred drawing. The maximal desired dimensions of the scene in each of the three dimensions can optionally be specified with the routine
void size3(picture pic=currentpicture, real x, real y=x, real z=y,
bool keepAspect=pic.keepAspect);
The resulting simplex linear programming problem is then solved to
produce a 3D version of a frame (actually implemented as a 3D picture).
The result is then fit with another application of deferred drawing
to the viewport dimensions corresponding to the usual two-dimensional
picture size parameters. The global pair viewportmargin
may be used to add horizontal and vertical margins to the viewport
dimensions.
For convenience, the three module defines O=(0,0,0),
X=(1,0,0), Y=(0,1,0), and Z=(0,0,1), along with a
unitcircle in the XY plane:
path3 unitcircle3=X..Y..-X..-Y..cycle;
A general (approximate) circle can be drawn perpendicular to the direction
normal with the routine
path3 circle(triple c, real r, triple normal=Z);
A circular arc centered at c with radius r from
c+r*dir(theta1,phi1) to c+r*dir(theta2,phi2),
drawing counterclockwise relative to the normal vector
cross(dir(theta1,phi1),dir(theta2,phi2)) if theta2 > theta1
or if theta2 == theta1 and phi2 >= phi1, can be constructed with
path3 arc(triple c, real r, real theta1, real phi1, real theta2, real phi2,
triple normal=O);
The normal must be explicitly specified if c and the endpoints
are colinear. If r < 0, the complementary arc of radius
|r| is constructed.
For convenience, an arc centered at c from triple v1 to
v2 (assuming |v2-c|=|v1-c|) in the direction CCW
(counter-clockwise) or CW (clockwise) may also be constructed with
path3 arc(triple c, triple v1, triple v2, triple normal=O,
bool direction=CCW);
When high accuracy is needed, the routines Circle and
Arc defined in graph3 may be used instead.
See GaussianSurface for an example of a three-dimensional circular arc.
The representation O--O+u--O+u+v--O+v--cycle
of the plane passing through point O with normal
cross(u,v) is returned by
path3 plane(triple u, triple v, triple O=O);
A three-dimensional box with opposite vertices at triples v1
and v2 may be drawn with the function
path3[] box(triple v1, triple v2);
For example, a unit box is predefined as
path3[] unitbox=box(O,(1,1,1));
Asymptote also provides optimized definitions for the
three-dimensional paths unitsquare3 and unitcircle3,
along with the surfaces unitdisk, unitplane, unitcube,
unitcylinder, unitcone, unitsolidcone,
unitfrustum(real t1, real t2), unitsphere, and
unithemisphere.
These projections to two dimensions are predefined:
-
oblique -
oblique(real angle) -
The point
(x,y,z)is projected to(x-0.5z,y-0.5z). If an optional real argument is given, the negative z axis is drawn at this angle in degrees. The projectionobliqueZis a synonym foroblique. -
obliqueX -
obliqueX(real angle) -
The point
(x,y,z)is projected to(y-0.5x,z-0.5x). If an optional real argument is given, the negative x axis is drawn at this angle in degrees. -
obliqueY -
obliqueY(real angle) -
The point
(x,y,z)is projected to(x+0.5y,z+0.5y). If an optional real argument is given, the positive y axis is drawn at this angle in degrees. -
orthographic(triple camera, triple up=Z) -
This projects from three to two dimensions using the view as seen at a point infinitely far away in the direction
unit(camera), orienting the camera so that, if possible, the vectoruppoints upwards. Parallel lines are projected to parallel lines. -
orthographic(real x, real y, real z, triple up=Z) This is equivalent to
orthographic((x,y,z),up).-
perspective(triple camera, triple up=Z, triple target=O) -
This projects from three to two dimensions, taking account of perspective, as seen from the location
cameralooking attarget, orienting the camera so that, if possible, the vectoruppoints upwards. Ifrender=0, projection of three-dimensional cubic Bezier splines is implemented by approximating a two-dimensional nonuniform rational B-spline (nurbs) with a two-dimensional Bezier curve containing additional nodes and control points. -
perspective(real x, real y, real z, triple up=Z, triple target=O) This is equivalent to
perspective((x,y,z),up,target).
The default projection, currentprojection, is initially set to
perspective(5,4,2).
A triple or path3 can be projected to a pair or path,
with project(triple, projection P=currentprojection) or
project(path3, projection P=currentprojection).
It is occasionally useful to be able to invert a projection, sending
a pair z onto the plane perpendicular to normal and passing
through point:
triple invert(pair z, triple normal, triple point,
projection P=currentprojection);
A pair z on the projection plane can be inverted to a triple
with the routine
triple invert(pair z, projection P=currentprojection);
A pair direction dir on the projection plane can be inverted to
a triple direction relative to a point v with the routine
triple invert(pair dir, triple v, projection P=currentprojection).
Three-dimensional objects may be transformed with one of the following built-in transform3 types:
-
shift(triple v) -
translates by the triple
v; -
xscale3(real x) -
scales by
xin the x direction; -
yscale3(real y) -
scales by
yin the y direction; -
zscale3(real z) -
scales by
zin the z direction; -
scale3(real s) -
scales by
sin the x, y, and z directions; -
scale(real x, real y, real z) -
scales by
xin the x direction, byyin the y direction, and byzin the z direction; -
rotate(real angle, triple v) rotates by
anglein degrees about an axisvthrough the origin;-
rotate(real angle, triple u, triple v) rotates by
anglein degrees about the axisu--v;-
reflect(triple u, triple v, triple w) reflects about the plane through
u,v, andw.
Three-dimensional TeX Labels, which are by default drawn as
Bezier surfaces directly on the projection plane, can be transformed
from the XY plane by any of the above transforms or mapped to a
specified two-dimensional plane with the transform3 types XY,
YZ, ZX, YX, ZY, ZX. There are also
modified versions of these transforms that take an optional argument
projection P=currentprojection that rotate and/or flip the
label so that it is more readable from the initial viewpoint.
A transform3 that projects in the direction dir onto the plane
with normal n through point O is returned by
transform3 planeproject(triple n, triple O=O, triple dir=n);
triple normal(path3 p);
to find the unit normal vector to a planar three-dimensional path p.
As illustrated in the example planeproject.asy, a transform3
that projects in the direction dir onto the plane defined by a
planar path p is returned by
transform3 planeproject(path3 p, triple dir=normal(p));
Three-dimensional versions of the path functions length,
size, point, dir, accel, radius,
precontrol, postcontrol,
arclength, arctime, reverse, subpath,
intersect, intersections, intersectionpoint,
intersectionpoints, min, max, cyclic, and
straight are also defined.
Here is an example showing all five guide3 connectors:
import graph3;
size(200);
currentprojection=orthographic(500,-500,500);
triple[] z=new triple[10];
z[0]=(0,100,0); z[1]=(50,0,0); z[2]=(180,0,0);
for(int n=3; n <= 9; ++n)
z[n]=z[n-3]+(200,0,0);
path3 p=z[0]..z[1]---z[2]::{Y}z[3]
&z[3]..z[4]--z[5]::{Y}z[6]
&z[6]::z[7]---z[8]..{Y}z[9];
draw(p,grey+linewidth(4mm)+opacity(0.5));
xaxis3(Label(XY()*"$x$",align=-3Y),red,above=true);
yaxis3(Label(XY()*"$y$",align=-3X),red,above=true);
dot(z);
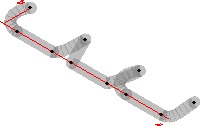
Three-dimensional versions of bars or arrows can be drawn with one of
the specifiers None, Blank,
BeginBar3, EndBar3 (or equivalently Bar3), Bars3,
BeginArrow3, MidArrow3,
EndArrow3 (or equivalently Arrow3), Arrows3,
BeginArcArrow3, EndArcArrow3 (or equivalently
ArcArrow3), MidArcArrow3, and ArcArrows3.
The predefined three-dimensional arrowhead styles are
DefaultHead3, HookHead3, TeXHead3.
Versions of the two-dimensional arrowheads lifted to three-dimensional
space and aligned according to the initial viewpoint are also defined:
arrowhead3 DefaultHead2(filltype filltype=Fill);
arrowhead3 HookHead2(real dir=arrowdir, real barb=arrowbarb,
filltype filltype=Fill);
arrowhead3 TeXHead2;
An unfilled arrow will be drawn if filltype=NoFill.
Module three also defines the three-dimensional margins
NoMargin3, BeginMargin3, EndMargin3,
Margin3, Margins3, BeginPenMargin3,
EndPenMargin3, PenMargin3, PenMargins3,
BeginDotMargin3, EndDotMargin3, DotMargin3,
DotMargins3, Margin3, and TrueMargin3.
Further three-dimensional examples are provided in the files
near_earth.asy, conicurv.asy, and (in the animations
subdirectory) cube.asy.
Limited support for projected vector graphics (effectively three-dimensional
nonrendered PostScript) is available with the setting
render=0. This currently only works for piecewise planar
surfaces, such as those produced by the parametric surface
routines in the graph3 module. Surfaces produced by the
solids package will also be properly rendered if the parameter
nslices is sufficiently large.
In the module bsp, hidden surface removal of planar pictures is
implemented using a binary space partition and picture clipping.
A planar path is first converted to a structure face derived from
picture. A face may be given to a two-dimensional drawing
routine in place of any picture argument. An array of such faces
may then be drawn, removing hidden surfaces:
void add(picture pic=currentpicture, face[] faces,
projection P=currentprojection);
Labels may be projected to two dimensions, using projection P,
onto the plane passing through point O with normal
cross(u,v) by multiplying it on the left by the transform
transform transform(triple u, triple v, triple O=O,
projection P=currentprojection);
Here is an example that shows how a binary space partition may be used to draw a
PostScript vector image of three orthogonal intersecting planes:
size(6cm,0); import bsp; real u=2.5; real v=1; currentprojection=oblique; path3 y=plane((2u,0,0),(0,2v,0),(-u,-v,0)); path3 l=rotate(90,Z)*rotate(90,Y)*y; path3 g=rotate(90,X)*rotate(90,Y)*y; face[] faces; filldraw(faces.push(y),project(y),yellow); filldraw(faces.push(l),project(l),lightgrey); filldraw(faces.push(g),project(g),green); add(faces);
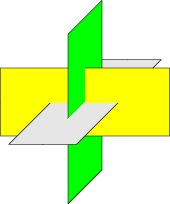
| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
